The most popular and widely used measure of representing the entire data by one value is what most laymen call the “average” and what statisticians call the arithmetic mean.
Its value is obtained by adding together all the items and then this total is divided by the number of items. The purpose of the mean is to describe the given data by a single value.
In this article, we list some of the merits and demerits of the simple arithmetic mean.
Advantages of Mean:
1) Simple to understand –
It is the simplest average to understand and easy to compute. The data is not required to be arranged in ascending or descending order as it is done when computing the median.
2) Depends on all values –
It is affected by the value of every item in the series. Therefore the mean can be said to truly represent the central tendency of the data.
Since all data values are used there is no loss of information. This is unlike the median or the mode which takes only some of the data values into consideration.
3) Rigidly defined –
It is calculated by a rigid algebraic formula that does not depend on the discretion of the researcher. This is important because if were not rigidly defined then the central value would be affected by the bias of the investigator.
4) It is capable of further algebraic treatment.
For example, if we are given the arithmetic mean and sizes of two groups we can find an algebraic formula for the mean of the combined group. This cannot be done for the median or the mode.
If we are given two groups of sizes n1 and n2 with the arithmetic means equal to X̄1 and X̄2 respectively then the combined mean can be calculated using the formula,
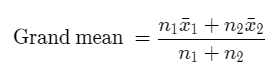
5) Mathematically significant –
The average has many significant mathematical properties. It occurs in important theorems in statistics such as the central limit theorem. The central limit theorem is widely used in the field of inferential statistics.
6) Not affected by sampling fluctuations –
It is reliable in the sense that it does not vary too much when repeated samples are taken from a big population for the purposes of estimation.
So if we wanted to estimate the average height of the population of a country it is enough to calculate the mean for a randomly chosen sample that is large enough. The sample mean will be a reliable estimate of the population mean.
7) Measures central tendency –
The mean is a “central value” for the data in the sense that the squares of differences of the data values from a numerical value A are the least when A is taken to be the simple arithmetic mean.
Thus we can say that the mean is the best measure of the central tendency of the data because it minimizes the “distance” of each observation from the central value.
8) Weighted average –
If some items in a distribution are more important than others we can assign “weights” to them and calculate the weighted arithmetic mean. The concept of “weights” is not useful when calculating the median or mode.
9) Wide Applications –
It has applications in fields such as economics, the stock market, education, and research. For example, we use the arithmetic mean in order to calculate the expected future gains of our stocks.
It is used in the field of education when for instance the teacher calculates the average score obtained by the students on a test.
Disadvantages of Mean:
1) Tedious calculations –
A limitation of the mean is that it cannot be determined by inspection like the mode. When finding the mode we can simply try to check which value occurs the most whereas finding the mean will require us to perform tedious calculations.
2) Cannot be found graphically –
Another drawback of the arithmetic mean is that it also cannot be located graphically unlike the median. The median can be located graphically by drawing a cumulative frequency polygon/ogive.
3) Not Suitable for Qualitative Data –
Arithmetic mean cannot be used when we are dealing with qualitative characteristics such as honesty, beauty, etc. Since we cannot measure these quantities numerically it becomes impossible to find the arithmetic mean for these quantities.
4) We cannot calculate the mean even if a single data value is missing.
This is a limitation because the median and mode can sometimes be calculated even when one of the values is missing. For example, suppose we are given the following set of data:
1, 1, 1, 1, 1, ?, 4, 8, 9.
Here the 6th data point is missing. But whatever the missing value it is clear that 1 is the value that is occurring in the data with the greatest frequency. So we conclude that the mode of the data is 1.
5) Not possible to calculate for open-ended Grouped Data –
It cannot be calculated for a grouped frequency distribution if the class intervals are open-ended. This is because we cannot calculate the mid-value for open-ended class intervals.
6) Not suitable for skewed distribution –
In an extremely asymmetrical/skewed distribution, the mean is usually not a suitable measure for the “central value” of the data.
7) Affected by extreme values –
The arithmetic mean sometimes gives a distorted picture of the data due to the presence of extreme values. Even if the data set contains a single data value that is very large, the mean will also be much larger compared to a true “central value” of the data.
8) Does not consider variability –
Two data sets can have the same arithmetic mean while having completely different implications.
For example, suppose Student A scores 55% on the first test, 60% on the second test, and 65% on the third test whereas Student B scores 65% on the first test, 60% on the second test, and 55% on the third test.
Both the students have the same average but the conclusion of the data set is not that the students are academically the same. Student A has shown consistent academic improvement whereas the performance of student B is becoming worse.
Thus one of the weaknesses of the mean is that we cannot blindly draw conclusions about the data by simply looking at the arithmetic mean.
We summarize the main merits and demerits of the arithmetic mean in the table below.
| Advantages of Mean | Disadvantages of Mean |
| It is based on all the observations. | It is affected by extreme values. |
| It is easily understood and easy to calculate. | Cannot be used when we are dealing with qualitative characteristics. |
| It is capable of further algebraic treatment. | Not suitable for skewed data sets. |
| Not affected by sampling fluctuations. | It cannot be calculated for distributions with open-end classes. |

Further Reading:
- Advantages, Disadvantages, and Uses of Median in Statistics.
- Properties of Mode – Uses and Advantages.
- Advantages, Disadvantages, and Uses of Geometric Mean.
