The Hausman test (also called the Durbin-Wu-Hausman test) is used to check whether an estimate for an unknown parameter is consistent or not.
It is also applied in the context of linear regression to decide whether to choose a fixed effect model or a random effect model.
How is Hausman’s test applied to check for the consistency of an estimator?
Step 1: Suppose we have a consistent estimator β0 for an unknown parameter value β. Further, assume that we manage to obtain a more efficient estimator β1.
Step 2: The null hypothesis of the Hausman’s test is that β1 is also a consistent estimator for β whereas the alternative hypothesis is that β1 is not a consistent estimator for β.
Step 3: We calculate the value of Hausman’s test statistic using the formula,
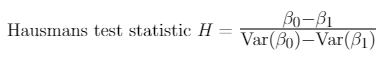
Hausman’s test statistic asymptotically follows the Chi –squared distribution.
Step 4: Using the value of the test statistic we obtain the p-value. If the p-value is less than the level of significance we reject the null hypothesis, otherwise we accept the null hypothesis.
Step 5: Alternatively, we compare the value of the test statistic with the critical table value. If the value of the test statistic exceeds the critical table value we reject the null hypothesis otherwise we accept the null hypothesis.
Applying Hausman’s test to decide for Fixed Effects Model vs Random Effects Model:
Consider the linear regression model,
Y = βX + c + ε where, ε denotes the error.
We have two estimators’ β0 and β1 under the fixed and the random-effects models respectively.
The null hypothesis for Hausman’s test, in this case, is that we use the random-effects model because it is more efficient. On the other hand, the alternative hypothesis tells us that we should use the fixed effects model since the random effect model is not consistent.
By applying the procedure for Hausman’s test given above we can decide which model (Fixed Effects vs Random Effects) is better.
We can also apply Hausman’s test to check for the endogeneity of variables in a regression model.