Uniform Distribution – Definition and Examples

The uniform distribution refers to a probability distribution in which all events have equal chances of occurring.

The continuous uniform distribution consists of two parameters – ‘a’ which denotes the minimum value the random variable can take and ‘b’ which denotes the maximum value that the random variable can take.

The pdf of the uniform distribution looks like this,

f(x)= 1/(b-a)     where, a<x<b

The graph of the pdf of uniform distribution looks like this,

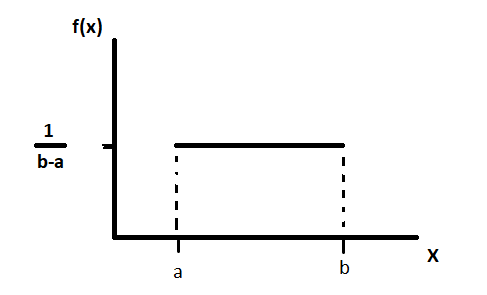
Because of the shape of the graph of the above pdf, the uniform distribution is also called the rectangular distribution

The expectation of the uniform distribution is given by the formula,

E(X) = (a+b)/2, that is, the average of the highest and lowest values.

The variance of the uniform distribution is given by the formula,

V(X)= (b-a)²/12

Use of Uniform Distribution:

1. An important property of uniform distribution is that if X is any random variable the CDF F(X) has a uniform distribution. Hence we use uniform distribution in simulation theory for the generation of random numbers following a particular distribution.
2. The uniform distribution is sometimes used to model the inter-arrival time between customers in certain highly theoretical queuing models.

The formula for calculating probability in uniform distribution:

If X follows uniform distribution then,

P(X<x)=(x-a)/(b-a)

Example:

If X follows a uniform distribution with parameters 13 and 17 find P(X<14). Also, find the expectation and variance of X.

Solution: We apply the formulae to get,

P(X<14)=(14-a)/(b-a) = 14-13/17-13 = ¼ = 0.25

E(X) = (a+b)/2 = 30/2 = 15

V(X)= (b-a)²/12 = 16/12 = 1.334

Remarks:

1. The difference between two uniform random variables follows the triangular distribution.
2. If X follows uniform distribution U(0,1) then –log X follows the exponential distribution.
3. The sum of two uniform random variables follows the Irwin Hall distribution.