Poisson Distribution – Formula & Examples

The Poisson distribution is a discrete probability distribution that is used to model real-life events that occur rarely or in situations where the probability of an event occurring is proportional to the time which has passed.

For example, we use may use the Poisson distribution to model the number of accidents that might occur on a particular street every year.

The Poisson distribution is used when there are we wish to model events that can theoretically occur infinitely many times (unlike the binomial distribution where the total number of trials n is some fixed finite number) but occur rarely in real life.

Poisson Distribution PMF (Probability Mass Function):

We can use the probability mass function of the distribution to calculate the probability associated with a Poisson random variable. The Poisson distribution is defined by a single parameter λ. The probability mass function of the Poisson distribution is given as,

P(X=x) = e^–λ λ^x/x! where x=0, 1, 2, 3,…

All Poisson distributions are skewed towards the right. As λ increases the distribution shifts more towards the right.

This is why the Poisson distribution has been called the probability distribution of rare events (the probabilities tend to be high for small numbers of occurrences).

The mean and variance of the distribution are both equal to the value of the parameter λ.

If X and Y are Poisson random variables with means λ₁ and λ₂ respectively then X+Y also follows a Poisson distribution with mean λ₁+ λ₂. This property is called the additive property of the Poisson distribution.

Poisson Distribution Example:

Suppose that an average of 3 car accidents occur per year on a particular street. Assume that the number of car accidents that occur is distributed in a Poisson manner. Calculate the probability that two or fewer accidents occur on the street in a particular year.

Solution:   Let X denote the number of car accidents that occur per year.

We are given that Mean = λ =3.

Then the probability mass function is P(X=x) = e^–3 3^x/x!.

Required probability = P(X=0) + P(X=1) + P(X=2)

= e^–3 3⁰/0! + e^–3 3¹/1! + e^–3 3²/2!   = 0.4231.

So there is a 42.31% chance that two or fewer accidents occur per year.

Mean and Variance of Poisson Distribution:

The mean and variance of the Poisson distribution are both equal to the parameter value λ.

E(X) = λ.

V(X) = λ.

The derivation of the mean and the variance is given below.

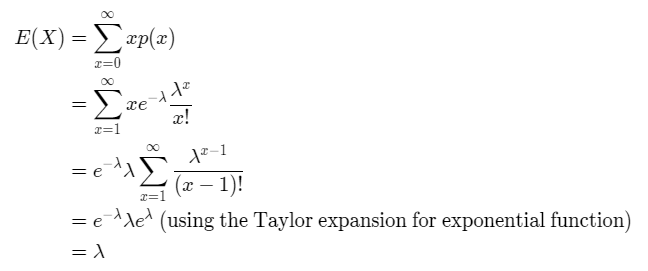
When to use Poisson Distribution:

The Poisson distribution can be used to model the following processes:

1. The number of deaths from a disease such as heart attack per year.
2. Used in quality control statistics to count the number of defects of an item.
3. The number of typographical errors on a page of a book.
4. In insurance problems to count the number of casualties.
5. The number of calls per minute received by a call center.
6. Number of customers per hour who arrive at a busy restaurant for dinner.
7. In physics to count the number of particles emitted by a radioactive substance

Poisson Distribution as an approximation for Binomial distribution:

Poisson distribution was discovered by the French mathematician and physicist Simeon Poisson who published it in 1837.

Poisson distribution can be used to approximate the binomial distribution under the following conditions:

1. n, the number of trials is indefinitely large
2. p, the constant probability of success for each trial is indefinitely small
3. np = A, (say), is finite where A is the mean.

What is lambda in Poisson Distribution?

The lambda in the Poisson distribution refers to the mean and the variance of the distribution.

What is e in poisson distribution?

The ‘e’ in the exponential distribution refers to the Eulers number whose approximate value is 2.718.