Degenerate Distribution (One Point Distribution)

Degenerate Distribution/One Point Distribution refers to a probability distribution of a random variable that takes only a single value with probability 1.

Since the random variable can only take one value the probability of the variable taking any other value is always zero.

We say that a probability distribution is non-degenerate if it is not a degenerate one-point distribution. This means that a non-degenerate random variable can take two or more possible values.

Probability Distribution of Degenerate Distribution:

We say that a random variable is degenerate at the point ‘k’ if the PDF is given as,

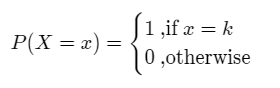
The cumulative distribution function F(x) is given as,

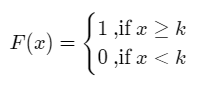
Mean and Variance:

The mean of the random variable X is equal to k. The expected value is equal to k because the random variable is certain to attain the value k.

Since the random variable is essentially constant, the variance is zero. Therefore, the variance of a degenerate distribution is always 0.

The converse statement is also true. If a discrete distribution has zero variance then we can conclude that it is a one-point degenerate distribution.

Raw moments:

The raw moments of the distribution are E(X^m) = k^m for m= 1, 2, 3…

Moment Generating Function:

The moment generating function of the distribution is, M_X(t) = e^tk.

Uses:

This distribution is not of much practical use in real life. It is a useful mathematical tool in the higher study of statistics.

The degenerate random variable plays a very important role in the study of limit theorems in probability theory.

Examples:

1. Suppose a coin is tossed. Let X be a random variable that takes the value 100 if either a head or tail occurs and is zero otherwise. Then it is clear that the random variable can only take the value 100 because it is certain that either head or tail will occur. Therefore the random variable X follows the degenerate distribution.
2. Let X be a random variable that takes the value 1 if the number on a dice thrown is less than 10 and zero otherwise. Since a die can only take the possible values 1, 2, 3, 4, 5, and 6 we conclude that the event is certain to occur and the random variable is certain to take the value 10.