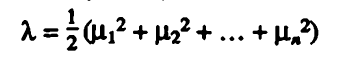Noncentrality parameter is a value that describes how far a probability density curve has been shifted from the usual central value.
The usual central distributions that we are familiar with such as Chi-square distribution, T distribution, and F distribution all have a fixed centre.
By the use of the noncentrality parameter, these distributions can be shifted to the left or right depending on the value chosen for the noncentrality parameters. The resulting distributions so obtained are called non-central Chi-squared (or non-central T/non central F) distributions.
By putting the value of the noncentrality parameter to 0 we get back our original central version of the distribution.

As we can see in the above picture the chi-square distribution shifts more and more to the right as the value of the noncentrality parameter increases.
Use in hypothesis testing:
The noncentrality parameter is very useful in the testing of hypothesis. It can be used when the null hypothesis is false and the parameter takes nonzero values.
In this case, the noncentrality parameter measures the extent to which the null hypothesis is false. It measures the degree to which the parameter value has shifted from zero.
Non centrality parameter of Chi-squared distribution:
The usual Chi-square distribution is obtained by summing up squares of normal random variables each with mean 0 and variance 1.
If we sum squares of normal random variable each and variance 1 but with means equal to µ1, µ2,…µn, respectively then we obtain the non-central Chi-squared distribution.
The noncentrality parameter of the non-central chi-squared distribution is given as,