The hypergeometric distribution is a discrete probability distribution that arises when we try to draw a random sample without replacement from a given population. For example, suppose there are N balls in a bag out of which M are white and the remaining N-M are black. Suppose we choose a sample of size n from the bag. Then the probability that the sample has k white balls can be calculated using the pdf of the hypergeometric distribution.
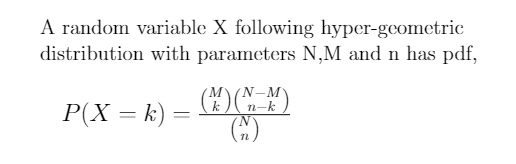
Example: Suppose that a bag contains 10 balls out of which 6 are white and 4 are black. If we choose 4 balls randomly from the bad then calculate the probability that two of these balls are white.
Solution: Let X denote the number of white balls in our sample.
Given N=10, M=6, n=4, and k=2.
Substituting all this in the above formula we get,
P(X=2) = (62)*(42)/(104) = 15*6/210 = 90/210 = 0.429
Mean and Variance of Hypergeometric Distribution:
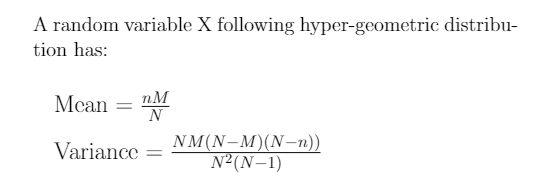
Example: In the above example, calculate the mean number of white balls selected and the variance.
Solution: Given N=10, M=6, n=4 and k=2.
Substituting all this in the above formula we get,
Mean = 4*6/10 = 2.4 ,that is, 2.4 white balls will be chosen on average.
Variance = (10*6*4*6)/(100*9) = 1.6
Use of hypergeometric distribution:
- It is used in the theory of Quality control to calculate the number of lots to be selected for inspection of quality of goods.
- It is used in sampling theory to calculate the probabilities of selecting particular kinds of samples without replacement.
Binomial approximation to Hypergeometric Distribution:
As the value of N tends toward infinity and the value M/N approaches a finite number then the hypergeometric distribution can be approximated using the pdf of the binomial distribution with parameters n and p=M/N.