The continuity correction factor is the change we make in the value of the variable by adding or subtracting 0.5 in order to calculate probabilities whenever a discrete random variable is being approximated by a continuous random variable.
For example, if we use the normal approximation to binomial or the normal approximation to the Poisson distribution we would necessarily have to add or subtract the correction factor.
Why do use the continuity correction factor?
Consider the following example. Suppose you throw a coin 100 times and you want to calculate the probability that you get heads 60 times. Let X denotes the number of heads.
To calculate P(X=60) if we were to directly use the normal distribution without the correction factor, we would get that the probability of getting 67 heads is 0. This is because since a continuous distribution takes uncountably many infinite values, the probability that it takes a particular value is 0. But this is clearly absurd since getting 67 heads is clearly NOT an impossible event. Hence we add and subtract 0.5 and calculate P (66.5<X<67.5) when using the normal approximation.
To avoid the king of absurd answers at above we use the correction factor whenever a discrete variable is approximated by a continuous distribution.
How to use the continuity correction factor?
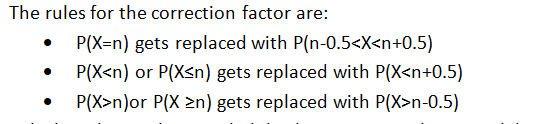
Examples of using continuity correction factor according to the above rules:
- Suppose that an archer tries to hit a target 500 times with probability of successfully hitting the target being 70%. To calculate the probability of hitting the target exactly 300 times using the normal approximation, we use the first rule given above and calculate P(299.5<X<300.5) using the normal distribution.
- To calculate the probability of hitting the target less than 432 times using the normal approximation, we use the second rule given above and calculate P(X<432.5) using the normal distribution.
- To calculate the probability of hitting the target greater than or equal to 124 times using the normal approximation, we use the third rule given above and calculate P(X>123.5) using the normal distribution.