In calculating arithmetic’ mean we suppose that all the items in the distribution have equal importance. But in practice, this may not be so.
If some items in a distribution are more important than others, then this point must be kept in mind, in order that the average computed is representative of the distribution.
In such cases, proper weightage is to be given to various items the weights attached to each item being proportional to the importance of the item in the distribution.
For example, if we want to have an idea of the change in the cost of living of a certain group of people, then the simple mean of the prices of the commodities consumed by them will not do, since all the commodities are not equally important, e.g., wheat, rice, and pulses are more important than tea, confectionery, etc.
A weighted mean is used when the values of the data set are not all equally represented.
A weighted mean allows you to assign more weight to certain values and less weight to others.
The weighted mean is a kind of arithmetic mean where we attach “weights” to the data values in accordance with their importance.
The main disadvantage of the simple arithmetic mean is that all data values are given equal importance in which case the mean may vary wildly even if one data point is replaced by an extremely low or high value.
The weighted mean deals with these problems by making sure that the average is not affected by outlier values.
How to Calculate the Weighted Mean:
The weighted arithmetic mean can be calculated using the formula,
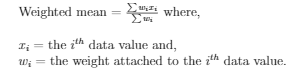
It is important to choose the correct weights when doing the calculation. If the weights are given then we can simply use them.
But if the weights are not given then we can use our understanding of the phenomena under study to “assign weights” to the data points.
Example:
Suppose we are given the following data for which we want to calculate the weighted arithmetic mean:
| Data values(xi) | Weights(wi) |
| 12 | 3 |
| 13 | 5 |
| 14 | 7 |
| 15 | 4 |
| 16 | 1 |
Solution: We calculate the required values as follows,
| Data values(xi) | Weights(wi) | xi*wi |
| 12 | 3 | 36 |
| 13 | 5 | 65 |
| 14 | 7 | 98 |
| 15 | 4 | 60 |
| 16 | 1 | 16 |
| ∑wi = 20 | ∑ xiwi = 275 |
Substituting all this in the above formula we get,
Weighted mean = ∑xiwi / ∑wi= 275/20 = 13.75
Remarks:
- The weighted mean is used in the calculation of index numbers and to calculate standardized birth and death rates.
- The weighted mean is equal to the simple mean if the weights assigned to each of the variate values are equal. It results in a higher value than the simple mean if smaller weights are given to smaller items and larger weights to larger items. If the weights attached to larger items are smaller and those attached to smaller items are larger, then the weighted mean results in a smaller value compared to the simple mean.