The coefficient of variation is a measure of dispersion that tells us about the “spread” of our data.
It tells us whether there is a high variation with the given data values or not. The higher the coefficient of variation the higher the spread of the data values.
If a given data set has a high coefficient of variation then we say the data are less consistent. For example, suppose we collect data about the number of hours a student studies per day for a hundred days.
If the variation is high that would mean the student is not consistent in the number of hours he spends studying each day.
Formula for calculating the Coefficient of Variation:
Coefficient of Variation C.V = Mean/Standard Deviation x 100% = x̄/σ x 100%
We see that the coefficient of variation is the ratio between the standard deviation and the mean expressed in percentage.
Steps to calculate Coefficient of Variation for given Data:
- Calculate the mean of the data using the formula, x̄ = ∑xi /n where xi denotes the sample values and n denotes the size of the sample.
- Calculate the standard deviation of the data set as shown in the example below.
- Divide the standard deviation by the mean and multiply the result by 100 to get the required value.
Example 1:
Calculate the coefficient of variation for the given set of data:
5, 6, 9, 8, 12, 14
Solution: We calculate the coefficient of variation in three steps as shown below:
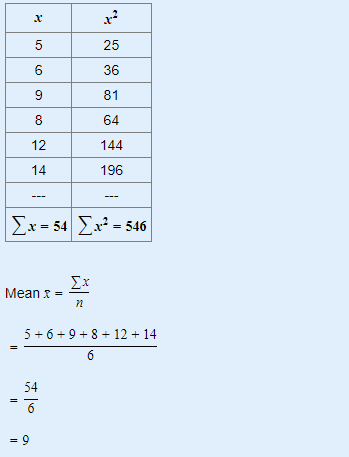
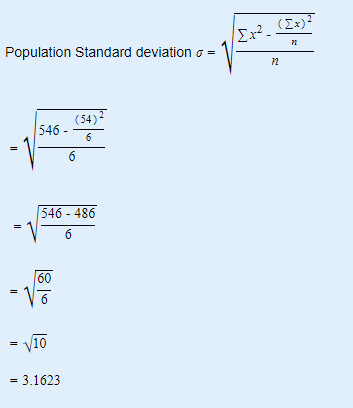
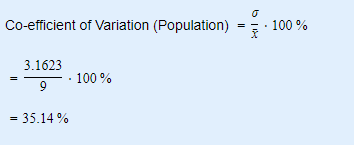
Hence there is a variation of 35.14% in the given data.
Let us look at another example of calculating the coefficient of variation.
Example 2:
Calculate the coefficient of variation for the given set of data:
35, 54, 52, 53, 56, 58, 52, 50, 51, 49
Solution: Step 1: We first calculate the mean of the data using the formula,
x̄ = ∑xi /n = 510/10 = 51
Step 2: Then we calculate the standard deviation using the formula,
Standard Deviation σ =√35 = 5.916
Step 3: Coefficient of Variation(C.V) = Mean/Standard Deviation *100 = 11.6%
Hence there is a variation of 11.6% in the given data.